투 포인터 알고리즘
포인터 두 개를 이용하여 문제를 해결하는 방법
전체 배열에서 연속하는 부분합(구간합)이 특정값 M와 일치하는 경우의 수를 구할 때 사용
만약에 연속하는 부분합을 구하는 문제에서 투 포인터 알고리즘을 사용하지 않으면, 이중 반복문이 필요하기 때문에
시간복잡도가 O(N²) 가 된다.
그러나 투 포인터 알고리즘을 사용하면 O(N) 으로 줄일 수 있음
투 포인터 알고리즘은 크게
1. 두 포인터가 같은 방향으로 진행하는 방법
2. 두 포인터가 다른 방향으로 진행하는 방법
두 가지로 나눌 수 있다.
이번에는 우선 두 포인터가 같은 방향으로 진행하는 방법에 대해 다룰 것이다.
투 포인터 알고리즘 시간복잡도 : O(N)
투 포인터 알고리즘에서 필요한 프로퍼티 :
- 부분합의 시작 인덱스를 가리키는 start 포인터
- 부분합의 마지막 인덱스를 가리키는 end 포인터
- start 지점부터 end-1 지점까지의 값을 모두 더한 결과를 저장하는 sum 변수
알고리즘 :
1. arr[start] ~ arr[end-1]까지의 구간합이 M과 같은 경우 :
카운트를 하나 증가시킴
2. arr[start] ~ arr[end-1]까지의 구간합이 M보다 크거나, end = arr.length 인 경우 :
구간합에서 arr[start] 값을 빼고, start 포인터를 하나 증가시킴
-> end = arr.length 인 경우에는 더 이상 end 포인터를 증가시킬 수 없으므로 start만 하나씩 증가시킨다
3. arr[start] ~ arr[end-1]까지의 합이 구간합 M보다 작은 경우 :
구간합에서 arr[end] 값을 더해주고, end 포인터를 하나 증가시킴
[예제]
배열의 크기가 6인 배열 arr의 원소가 순서대로 1 2 3 4 2 6 이고,
이 배열에서 부분합(M)이 6이 되는 경우의 수를 구하여라.
제일 먼저 start = 0, end = 0, sum = 0, cnt = 0 으로 초기화한다.

sum < M 이므로, sum +=arr[end++] 을 수행한다.
sum에 arr[0]을 더하고 end는 1로 증가
start = 0, end = 1, sum = 1, cnt = 0

sum < M 이므로, sum에 arr[1]을 더하고 end는 2로 증가
start = 0, end = 2, sum = 3, cnt = 0

sum < M 이므로, sum에 arr[2]를 더하고 end는 3으로 증가
start = 0, end = 4, sum = 6, cnt = 0

드디어 처음으로 sum = M이 되었다. 부분합이 M과 같아졌으므로 카운트는 하나 증가시킨다.
이제 1번 인덱스를 시작 위치로 해서 또 M과 같아지는 부분합을 찾아나갈 것이다.
그러므로 sum에서 arr[0]을 빼고 start을 1로 증가시킨다.
start = 1, end = 4, sum = 5 cnt = 1

sum < M 이므로, sum에 arr[3]을 더하고 end를 4로 증가
start = 1, end = 4, sum = 9, cnt = 1

sum > M 이므로, sum에 arr[1]을 빼고 start을 2로 증가
start = 2, end = 4, sum = 7, cnt = 1
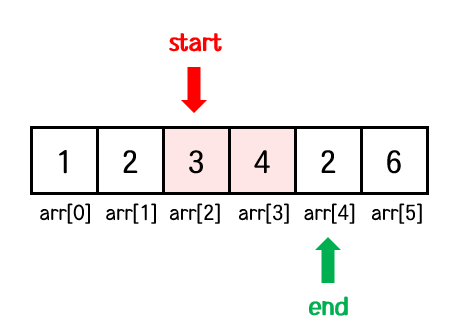
sum > M 이므로, sum에 arr[2]를 빼고 start를 3으로 증가
start = 3, end = 4, sum = 4, cnt = 1

sum < M 이므로, sum에 arr[4]를 더하고 end를 5로 증가
start = 3, end = 5, sum = 6, cnt = 1

sum이 6이 되어 sum = M 이다. 그러므로 cnt를 하나 증가시킨다.
sum에서 arr[3]을 빼고 start는 4로 증가시킨다.
start = 4, end = 5, sum = 2, cnt = 2

sum < M이므로, sum에서 arr[5]를 더하고 end를 6으로 증가
start = 4, end = 6, sum = 8, cnt = 2

sum > M이므로, sum에서 arr[4]를 빼고 start를 5로 증가
start = 5, end = 6, sum = 6, cnt = 2

sum = M 이므로, cnt를 하나 증가시킨다.
sum에서 arr[5]를 빼고 start를 6으로 증가
start = 6, end = 6, sum = 0, cnt = 3

start이 6이 되어 배열의 크기보다 커졌으므로 반복문을 종료한다.
최종적으로 부분합이 6이 되는 경우는 3번이다.
핵심 소스코드 :
public static int getCount(int[] arr) {
int start = 0, end = 0;
int sum = 0;
int cnt = 0;
while (start < arr.length) {
if (sum == M) {
cnt++;
sum -= arr[start++];
} else if (sum > M || end == N)
sum -= arr[start++];
else
sum += arr[end++];
}
return cnt;
}
반복문의 탈출 조건은 start 포인터가 배열의 크기보다 작을 때(start<N)이다.
개인적으로 반복문의 탈출 조건이 헷갈렸었다. 반복문의 탈출조건이 end<N 이어야 하는 것 아닌가?라고 생각했었다.
하지만 주의해야할 것이 end 포인터가 배열의 마지막까지 도착했다고 하더라도 반복문을 끝내서는 안된다.
end = arr.length 이더라도, start 포인터가 하나씩 증가하는 과정에서
부분합 M과 일치하는 경우가 있을 수 있기 때문이다.
다음 소스코드는 투 포인터 알고리즘을 사용하여 풀이한 백준 2003번 문제다.
'Algorithm & DS > 투 포인터' 카테고리의 다른 글
| 투 포인터 알고리즘 - 2. 다른 방향(배열 2개) (0) | 2021.02.18 |
|---|---|
| 투 포인터 알고리즘 - 2. 다른 방향(배열 1개) (2) | 2021.02.16 |