병합 정렬(Merge Sort)
배열을 두 개로 쪼개어서 정렬을 한 뒤, 다시 병합하는 작업을 반복하는 정렬 알고리즘
배열을 중앙을 기준으로 앞(left ~ center)과 뒤(center+1 ~ right)로 나눈다. 이 작업을 배열의 요소가 2개가 될 때까지 반복한다.
나누어진 두 개의 배열을 정렬한 뒤 하나의 배열로 병합한다. 이렇게 배열을 모두 정렬 및 병합하면 종료한다.


시간복잡도 : O(NlogN)
퀵 정렬은 최악의 경우 시작복잡도가 O(N²) 이지만, 병합 정렬은 O(NlogN)로 유지된다.
[예제]
배열 arr의 요소가 5 9 3 1 8 6 4 7 2 일 때, 이 배열을 오름차순으로 정렬하기
먼저 배열 arr의 left = 0, right = arr.length -1 로 초기화해준다.
left는 배열의 맨 왼쪽 끝 인덱스이고, right는 배열의 맨 오른쪽 끝 인덱스이다.
그리고 center = (left + right) / 2 가 되어 center가 배열의 중앙 인덱스를 담도록 한다.

< 배열 나누기>
병합 정렬은 먼저 배열을 앞 뒤로 쪼개는 작업을 해야하는데, 이 작업은 재귀를 이용하여 구현할 수 있다.
mergeSort(arr, left, center);
mergeSort(arr, center+1, right);
mergeSort()의 첫번째 인수는 정렬할 배열이고, 두번째 인수는 쪼개진 배열의 맨 왼쪽 인덱스,
세번째 인수는 쪼개진 배열의 맨 오른쪽 인덱스가 들어간다.

이렇게 앞과 뒤로 나누어진 배열은 또 다시 재귀를 반복하며 left ~ center, center+1 ~ right 로 쪼갠다.
재귀를 사용할 때는 베이스 케이스가 있어야 한다.
병합 정렬에서는 배열을 더 이상 쪼갤 수 없을 때가 베이스 케이스가 될 것이다.
즉, left < right 조건을 만족할 때까지 배열을 쪼갤 수 있을 것이다.
left = right 이면 쪼개진 배열의 요소가 한 개밖에 없기 때문에 더 이상 배열을 쪼갤 수 없다. 그러므로 재귀를 종료한다.
= 배열의 divide를 종료한다.

< 정렬 및 병합하기>
이제 나누어진 배열을 정렬 -> 병합을 할 차례이다.먼저 left = 0 ,right = 1 인 범위부터 정렬한다.

버퍼를 하나 생성한다. 버퍼의 크기는 쪼개어진 앞쪽 배열의 크기(center - left + 1)만큼 할당한다.
int[] buf = new int[center - left + 1];
위의 그림에서 앞쪽 배열의 크기는 1이다. 그러므로 버퍼의 크기는 1이 된다.
그 다음, 앞쪽의 배열의 요소를 모두 버퍼에 담는다.

pl, pr 변수를 만들어서 pl은 버퍼의 가장 왼쪽을 가리키고, pl = 0
pr은 뒤쪽 배열의 가장 왼쪽을 가리키도록 한다. pr = center+1
(뒤쪽 배열의 가장 첫번째 인덱스는 center+1 이었다.)
그리고 idx 변수를 생성하여, 현재 배열 arr에서 정렬을 하려고하는 범위의 첫번째 위치를 담는다.
현재 정렬을 하려고하는 범위는 left = 0 ~ right = 1 이므로 idx = 0 이 들어간다.
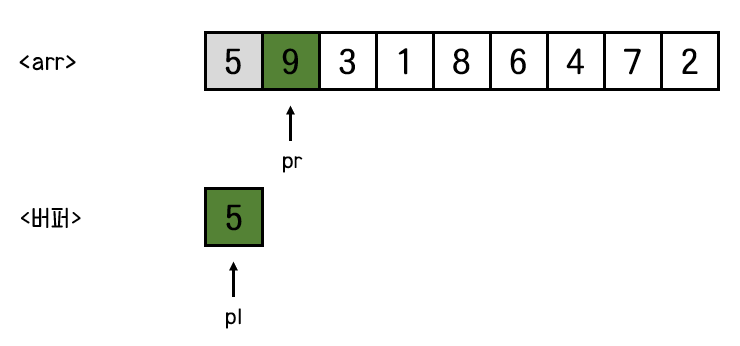
이제부터 버퍼의 pl이 가리키는 값과 arr의 pr이 가리키는 값의 대소관계를 비교하여 더 작은 값이 arr의 left부터 차례대로 담길 것이다.
pl이 가리키는 값이 더 작으면 arr[idx] = buf[pl] 이 들어가고, pl은 버퍼의 다음 위치로 이동한다.
pr이 가리키는 값이 더 작으면 arr[idx] = arr[pr] 이 들어가고, pr은 arr의 다음 위치로 이동한다.
pl이 가리키는 값 < pr이 가리키는 값 -> arr[idx++] = buf[pl++];
pl이 가리키는 값 > pr이 가리키는 값 -> arr[idx++] = buf[pr++];
이 과정을 pl이 버퍼의 범위를 벗어나거나, pr이 범위를 벗어날 때까지 반복한다.
여기서는 buf[pl] < arr[pr] 이므로 arr[0] = buf[pl] = 5 가 들어간다. 그리고 pl은 하나 증가하여 1이 된다.
pl 이 버퍼의 범위를 벗어났으므로 반복문이 종료된다.

반복문이 종료된 후에도 pl이 아직 버퍼의 범위 안에 있는 경우(pl < buf.length)에는
pl을 끝까지 이동시키며 버퍼의 요소를 arr에 차례대로 담는다.
여기서는 pl이 이미 버퍼의 범위를 벗어났기 때문에 더 이상 작업을 진행하지 않고 정렬을 종료한다.

이제, left = 0, right = 2 인 범위를 정렬해보자.

마찬가지로 배열을 쪼개었을 때, 앞쪽에 해당하는 배열의 요소를 버퍼에 옮겨담는다.

pl = 0, pr = 2, idx = 0 으로 초기화한다.
그리고 buf[pl]과 arr[pr]을 비교하면서 더 작은 값을 arr[idx]에 넣는 작업을 반복한다.

buf[0] > arr[pr] 이므로 arr[0] 에는 arr[pr] = 3 이 들어간다. 그리고 pr은 하나 증가하여 3이 된다.
pr이 right = 2보다 크므로 범위를 벗어났으므로 바로 반복문이 종료된다.

반복문이 종료된 후, pl은 여전히 버퍼의 범위 안에 있다. pl < buf.length
그러므로 pl을 이동시키면서 버퍼의 값들을 arr[1]부터 시작하여 차례대로 옮겨담는다.

버퍼의 값들을 모두 옮겨담으면, left = 0 부터 right = 2 까지 범위의 정렬 및 병합이 완료된다.
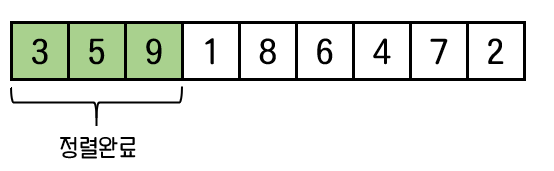
나머지 과정도 위와 동일하다.
left = 0 ~ right = 4 범위의 정렬 & 병합이 완료된 상태이고,
left = 5 ~ right = 8 범위의 정렬 & 병합이 완료된 상태라고 가정하고(과정은 위와 동일하므로 생략한다)
이 두 배열을 정렬 및 병합하는 과정을 마지막으로 보자.

left = 0, right = 8 인 범위(배열 전체)를 정렬 및 병합할 차례이다.
이 때, 앞쪽의 배열(초록색부분), 뒤쪽의 배열(파란색부분)은 각각 정렬을 마친 상태일 것이다.
버퍼를 생성하고 앞쪽의 배열 값들을 버퍼에 옮겨담는다.

pl = 0(버퍼의 맨 왼쪽 인덱스), pr = 5(뒤쪽 배열의 맨 왼쪽 인덱스 : center + 1), idx = 0 으로 초기화한다.

buf[0] < arr[5] 이므로 arr[0] = buf[0] = 1 이 들어간다. 그리고 pl이 하나 증가한다.
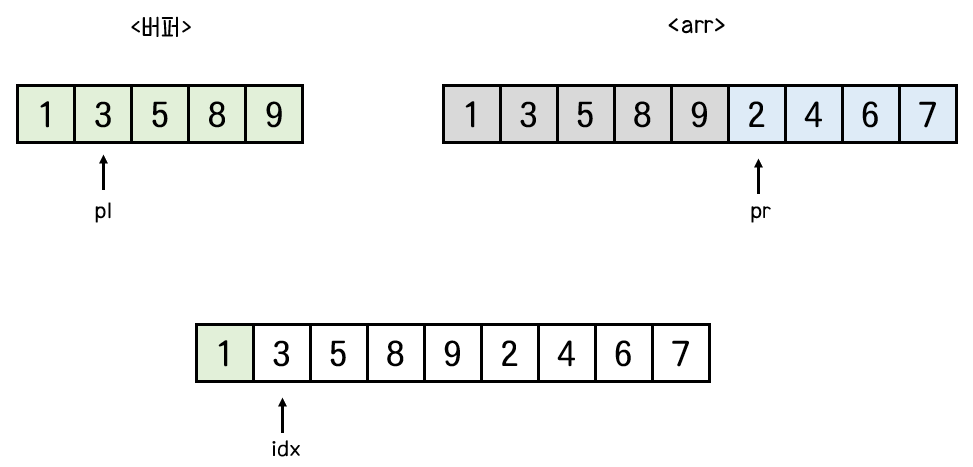
buf[1] > arr[5] 이므로 arr[1] = arr[5] = 2 가 들어가고, pr이 하나 증가한다.

buf[1] < arr[6] 이므로 arr[2] = buf[1] = 3 이 들어가고, pl이 하나 증가하여 2가 된다.

buf[2] > arr[6] 이므로 arr[3] = arr[6] = 4 가 들어가고, pr이 하나 증가하여 7이 된다.

buf[2] < arr[7] 이므로 arr[4] = buf[2] = 5 가 들어가고, pl이 하나 증가한다.
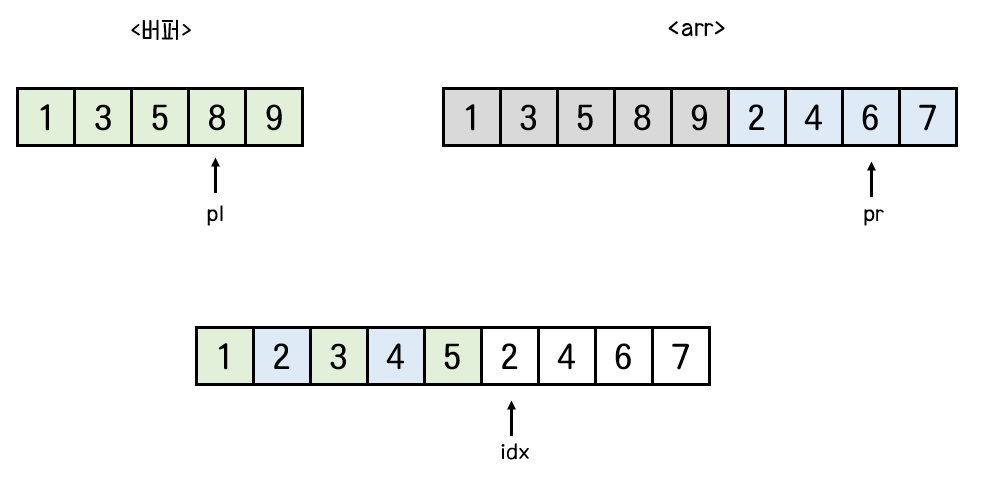
buf[3] > arr[7] 이므로 arr[5] = arr[7] = 6이 들어가고, pr이 하나 증가한다.

buf[3] > arr[8] 이므로 arr[6] = arr[8] = 7 이 들어가고, pr은 하나 증가하여 9가 된다.
여기서 pr이 범위를 벗어났으므로 반복문이 종료된다.

반복문이 종료된 후, pl을 보니 아직 버퍼의 범위 안에 있다. pl < buf.length
그러므로 버퍼의 나머지 값들을 arr[7]부터 차례대로 옮겨담는다.


최종적으로 배열 arr의 정렬이 완료된 것을 확인할 수 있다.

소스코드 :
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int center = (left + right) / 2;
// 배열 쪼개기
mergeSort(arr, left, center);
mergeSort(arr, center + 1, right);
// 정렬 및 병합
int size = center - left + 1;
int[] buf = new int[size]; // 버퍼 생성
for (int i = left; i <= center; i++)
buf[i - left] = arr[i];
int pl = 0, pr = center + 1;
int idx = left;
while (pl < size && pr <= right)
arr[idx++] = (buf[pl] < arr[pr]) ? buf[pl++] : arr[pr++];
while (pl < size)
arr[idx++] = buf[pl++];
}
}'Algorithm & DS > 정렬' 카테고리의 다른 글
| 힙 정렬(Heap Sort) (0) | 2021.02.22 |
|---|---|
| 퀵 정렬(Quick Sort) (2) | 2021.02.17 |
| 단순 삽입 정렬(Straight Insertion Sort) (0) | 2021.02.16 |
| 단순 선택 정렬(Straight Selection Sort) (0) | 2021.02.16 |
| 버블 정렬(Bubble Sort) (0) | 2021.02.16 |