1509번: 팰린드롬 분할
세준이는 어떤 문자열을 팰린드롬으로 분할하려고 한다. 예를 들어, ABACABA를 팰린드롬으로 분할하면, {A, B, A, C, A, B, A}, {A, BACAB, A}, {ABA, C, ABA}, {ABACABA}등이 있다. 분할의 개수의 최솟값을 출력하
www.acmicpc.net
문제를 풀기 위해 다음과 같은 두개의 배열을 생성했다.
dp[i] : 0부터 i번째 위치까지 팰린드롬 분할의 최소 개수
palindrome[j][i] : j번째부터 i번째까지의 문자열이 팰린드롬이면 true, 팰린드롬이 아니면 false
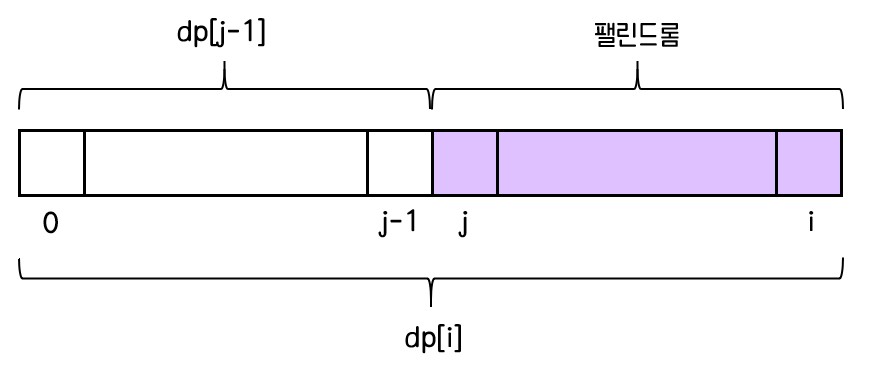
0번째부터 i번째까지 팰린드롬 분할의 최수 개수(dp[i])를 구하기 위해서는 0<=j && j<=i 일 때,
j+1번째부터 i번째까지 문자열이 팰린드롬이면서 dp[j]가 최소가 되는 경우를 찾아야 한다.
그리고 나서 +1을 해주면 dp[i]를 구할 수 있다.
점화식 : dp[i] = min(dp[j-1]) + 1
이해를 돕기 위해 예시를 들어보자.
입력으로 주어진 문자열이 BACABDDDD 라고 할 때, 최종적으로 구해야 하는 팰린드롬 최소 분할 개수는
dp[8]이 된다. dp[0]부터 dp[7]까지 모두 구했다고 가정하고, dp[8]을 구할 차례라고 하자.
j의 범위는 0부터 8까지 일 때, j+1부터 8번째까지 문자열이 팰린드롬이면서 dp[j]가 최소인 경우를 찾는 과정은 다음과 같다.
j = 7일 때, j(7)번째부터 i(8)번째까지 문자열 "DD"는 팰린드롬이다. 그리고 dp[j-1] = dp[6] = 2 이다.
(dp[6]는 이미 전단계에서 구했다고 가정 -> {BACAB}, {DD} )
이 때 dp[8]는 6번째 위치까지 구한 팰린드롬 분할 최소 개수(dp[6])에다가 +1을 더한 결과가 된다. 왜냐하면 "DD"는 팰린드롬이므로 더 이상 분할할 필요가 없는 그 자체로 하나의 분할로 여겨지기 때문이다.
dp[8] = dp[6] + 1 = 3

이번에는 j = 6 일 때를 보자.
j번째(6)부터 i(8)번째까지 문자열 "DDD"는 팰린드롬이다. 그리고 dp[j-1] = dp[5] = 2 이다.
({BACAB}, {D}로 쪼개는 경우가 최소 분할 개수이므로)
이 때의 dp[8]는 dp[5] + 1 = 3이 된다.

그 다음, j = 5일 때를 보자.
j(5)번째부터 i(8)번째까지 문자열 "DDDD" 역시 팰린드롬이다. 또한, dp[j-1] = dp[4] = 1 이다. {BACAB}
이 때의 dp[8] = dp[4] + 1 = 2가 된다.
총 {BACAB}, {DDDD} 두 가지로 분할할 수 있기 때문이다.

j = 4일 때를 보니, "BDDDD"는 팰린드롬이 아니다.
j = 3일 때, "ABDDDD"는 팰린드롬이 아니다.
j = 2일 때, "CABDDDD"는 팰린드롬이 아니다.
j = 1일 때, "ACABDDDD"는 팰린드롬이 아니다.
j = 0일 때, "BACABDDDD"는 팰린드롬이 아니다.
따라서, 여태까지 구한 dp[8]중에서 가장 최소가 되는 값은 j = 5일 때 dp[8] = 2 이므로, 최종 dp[8]는 2가 된다. 즉, 8번째까지 문자열의 팰린드롬 분할 최소 개수는 2개가 되는 것이다.
점화식 : dp[i] = min(dp[j-1]) + 1
그렇다면 이 점화식을 사용하여 메모이제이션을 하기 전에, j번째부터 i번째까지의 문자열이 팰린드롬인지 아닌지를 먼저 체크하는 과정이 선행되어야 한다. 따라서 전체 문자열을 차례대로 검사하면서 j번째부터 i번째까지 문자열이 팰린드롬인지를 사전에 확인하여, 팰린드롬이면 palindrome[j][i] = true, 아니면 palindrome[j][i] = false가 들어가도록 한다.
아래 코드는 전체 문자열에서 모든 팰린드롬을 찾아서 palindrome[j][i] = true를 해주는 메서드이다.
public static void checkPalindrome(String str, int len) {
for (int start = 1; start <= len; start++) {
for (int end = start; end <= len; end++) {
boolean flag = true;
int s = start - 1;
int e = end - 1;
while (s <= e) {
if (str.charAt(s++) != str.charAt(e--)) {
flag = false;
break;
}
}
if (flag)
palindrome[start][end] = true;
}
}
}
전체 코드 :
'BOJ' 카테고리의 다른 글
| [백준 11722번] 가장 긴 감소하는 부분 (java) (0) | 2019.09.21 |
|---|---|
| [백준 4949번] 균형잡힌 세상 (java) (0) | 2019.09.21 |
| [백준 1707번] 이분 그래프 (java) (0) | 2019.09.21 |
| [백준 9251번] LCS (java) (0) | 2019.09.20 |
| [백준 7569번] 토마토 (java) (0) | 2019.09.18 |