
1041번: 주사위
첫째 줄에 N이 주어진다. 둘째 줄에 주사위에 쓰여 있는 수가 주어진다. 위의 그림에서 A, B, C, D, E, F에 쓰여 있는 수가 차례대로 주어진다. N은 1,000,000보다 작거나 같은 자연수이고, 쓰여 있는 수
www.acmicpc.net
정육면체를 이루는 주사위를 3면이 다 보이는 경우, 2면만 보이는 경우, 1면만 보이는 경우 이렇게 3가지로 나눌 수 있다. 그리고 각각에 해당하는 주사위의 개수를 N에 대한 식으로 나타내면 다음과 같다.
-
3면만 보이는 주사위의 개수 : 4
-
2면만 보이는 주사위의 개수 : 8(N-2) + 4
-
1면만 보이는 주사위의 개수 : 5(N-2)^2 + 4(N-2)
3면이 보이는 주사위

3면이 보이는 주사위에서 최소값은 한 모서리를 공유하는 주사위의 세 면의 합이 최소가 되어야 한다.
그러기 위해서는 마주보는 두 면에 쓰여있는 수 중 더 작은 값을 선택해서 더하면 된다.
즉, A와 F 중에서 더 작은 값, B와 E 중에서 더 작은 값, C 와 D 중에서 더 작은 값을 더한다.
그리고 3면만 보이는 주사위의 개수는 4개이므로 더한 값에 4를 곱한다.
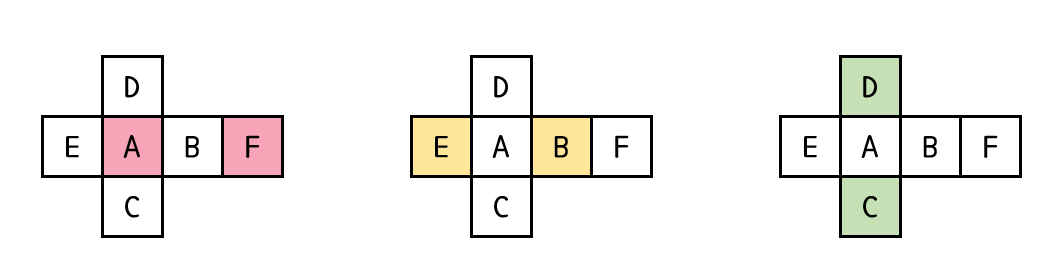
2면이 보이는 주사위

2면이 보이는 주사위에서 최소값은 주사위에서 인접한 두 면에 쓰여있는 합이 최소가 되는 경우이다.
이 때, 두 면이 인접한다는 것은 어느 한 면을 기준으로 봤을 때, 마주보는 면만 아니면 다 인접하다.
그러므로 마주보는 면인지 아닌지 확인한 후, 마주보는 면이 아니면 두 합을 구하고 더 작은 합이 나오면 계속 갱신해나간다.
최종적으로 구해진 가장 작은 두 면의 합에 8(N-2) + 4 만큼을 곱해준다.
1면이 보이는 주사위

마지막 1면만 보이는 주사위에서 최소값을 구하기 위해서는 주사위의 6면 중에서 가장 작은 수가 쓰여진 면이 보이면 되는 것이다. 그러므로 6개의 면을 비교하여 가장 가장 수를 선택한다. 그리고 1면만 보이는 주사위의 개수는 5(N-2)^2 + 4(N-2)개 이므로 5(N-2)^2 + 4(N-2) 만큼 곱해준다.
소스코드 :
'BOJ' 카테고리의 다른 글
| [백준 1201번] NMK (java) (0) | 2021.03.07 |
|---|---|
| [백준 1783번] 병든 나이트 (java) (0) | 2021.03.06 |
| [백준 9576번] 책 나눠주기 (java) (0) | 2021.03.04 |
| [백준 1744번] 수 묶기 (java) (2) | 2021.03.04 |
| [백준 1541번] 잃어버린 괄호 (java) (0) | 2021.03.04 |