
2873번: 롤러코스터
첫째 줄에 가장 가장 큰 기쁨을 주는 롤러코스터는 가장 왼쪽 위 칸부터 가장 오른쪽 아래 칸으로 어떻게 움직이면 되는지를 출력한다. 위는 U, 오른쪽은 R, 왼쪽은 L, 아래는 D로 출력한다. 정답
www.acmicpc.net
R : 홀수 OR C : 홀수
R, C 둘 중에 하나라도 홀수이면 모든 칸에 있는 기쁨을 다 더할 수 있다. 모든 칸을 다 방문할 수 있다.

R : 짝수 AND C : 짝수
문제는 R과 C 둘 다 짝수인 경우이다. R과 C 둘 다 짝수인 경우에는 모든 칸을 다 지날 수 없기 때문에 기쁨의 합이 최대가 되는 방법을 생각해야한다.
처음에는 dfs를 이용하여서 모든 가능한 경로를 다 탐색한 후에 기쁨의 합이 최대가 되는 경로를
출력하도록 했었다.
그러나 결과는 '메모리 초과'
혼자서는 도저히 방법을 모르겠어서 백준님의 강의자료를 참고하였다.
RxC 칸을 체스판처럼 검정과 흰색 칸으로 나누고 첫 (0, 0)을 흰색으로 시작한다고 할 때,
R, C 둘 중에 하나라도 홀수인 경우에는 아래 그림처럼 끝칸은 항상 검정색으로 끝난다.
그리고 모든 칸을 다 지나기 때문에 흰색칸을 짝수개만큼, 검정칸도 짝수개만큼 지나간다.

반면에 R와 C 둘 다 짝수인 경우에는 (0, 0)을 흰색으로 시작하면 끝칸도 반드시 흰색으로 끝난다.
칸에서 다른 칸으로 이동할 때 무조건 흰색 -> 검은색 혹은 검은색 -> 흰색으로만 이동이 가능하다.
그렇기 때문에 끝칸에 도착했을 때 흰색이라는 것은, 방문한 칸들 중 흰색칸이 검정색칸보다 하나 더 많이 방문했다는 것을 의미한다.
R과 C 둘 다 짝수이기 때문에 흰색에서 시작해서 흰색으로 도달하려면 검정칸을 하나 방문하지 않으면 된다. 그러면 방문한 흰색칸이 방문한 검정칸보다 하나 더 많게 되기 때문이다.

그러므로 검정칸 중에서 가장 작은 기쁨을 갖는 칸을 찾은 다음에, 그 칸을 제외한 모든 칸을 방문하면 된다.
이제 여기까지는 이해가 됐다치더라도, 경로를 어떻게 구현할 지가 또 다른 문제다.
경로를 구하는 방법은 다음과 같다.
시작칸과 끝칸에서 동시에 출발한다. 즉, 양쪽에서 동시에 출발해서 서로 만나면 되는 것이다.
두 행씩 움직이면서 둘 사이에 한 행 이상이 남아있을 때까지 반복한다.
그리고 앞으로 이동할 두 행에 최소 기쁨을 갖는 검정칸(mr, mc)이 존재하지 않아야 한다.


그런 다음, 방금까지는 좌우로 이동했다면 이번에는 같은 방법으로 위아래로 이동한다.
두 열씩 움직이면서 둘 사이에 한 열 이상이 남아있을 때까지 반복한다.
그리고 앞으로 이동할 두 열에 최소 기쁨을 갖는 검정칸(mr, mc)이 존재하지 않아야 한다.
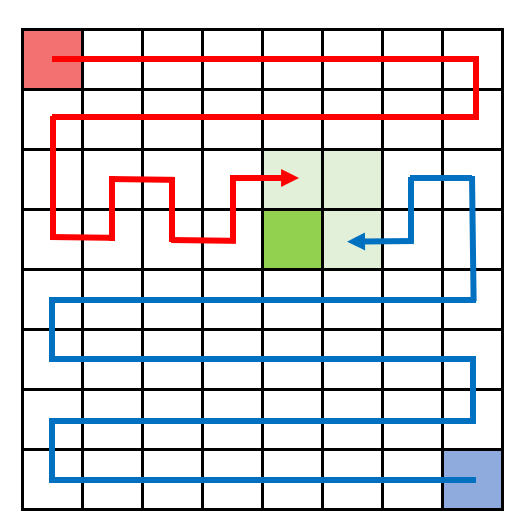
여기까지 진행했을 때, 빨간 화살표의 위치를 (sr, sc) 라고 하면, sc = mc 이면 빨간 화살표는 (mr, mc)를 피해서 움직여야 하므로 오른쪽으로 갔다가 아래쪽으로 내려간다. R -> D

sc != mc 라면 아래쪽으로 내려갔다가 오른쪽으로 이동한다. D -> R

소스코드 :
소스코드는 아래 블로그를 참조하여 작성했습니다.
백준 2873 롤러코스터 Java
정답률 29퍼센트의 그리디 문제이다. 매우 어려운 문제인 것 같고 어려워서 금방 까먹을 것 같기 때문에 백준님의 강의를 통해 정리하려 한다. r행 c열의 표 모양에서 가장 왼쪽 위 칸 부터 가장
dundung.tistory.com
'BOJ' 카테고리의 다른 글
| [백준 1992번] 쿼드트리 (java) (0) | 2021.03.09 |
|---|---|
| [백준 8983번] 사냥꾼 (java) (0) | 2021.03.08 |
| [백준 1080번] 행렬 (java) (0) | 2021.03.07 |
| [백준 1201번] NMK (java) (0) | 2021.03.07 |
| [백준 1783번] 병든 나이트 (java) (0) | 2021.03.06 |