LIS(Lowest Increasing Subsequence) - 길이 구하기

LIS(Lowest Increasing Subsequence) : 최장 증가 수열 

: 어떤 수열이 주어졌을 때, 그 수열에서 가장 긴 증가하는 부분 수열을 구하는 알고리즘

  (최장 증가 수열의 요소가 꼭 연속하지 않아도 됨)

 

 1. 최장 증가 수열을 나열하는 문제

 2. 최장 증가 수열의 길이를 구하라는 문제

 

보통 이 두가지 문제가 기본적이다.

여기서는 최장 증가 수열의 길이를 구하는 알고리즘을 볼 것이다. 1번 케이스의 경우, 수열 자체를 구하는 것이기 때문에 수열 요소의 추적이 별도로 필요하다.

 

시간 복잡도 : O(NlogN)

 

 

대략적인 알고리즘은 아래와 같다.

증가하는 수열을 저장하는 리스트가 필요하다. 리스트는 증가하는 수열을 저장하고 있기 때문에 계속 오름차순 상태를 유지하면서 갱신된다. 수열의 요소를 차례대로 탐색하면서 리스트에 해당 요소를 추가하거나, 원래 값을 해당 요소로 변경한다. 최종적으로 리스트의 크기가 가장 긴 증가하는 수열의 길이가 된다.

 

 

알고리즘 : 

입력받은 수열의 첫 번째 요소부터 차례대로 탐색한다(반복문)

 

리스트의 가장 마지막 값(list.get(list.size()-1))과 수열의 현재 요소(n)을 비교한다. 

(리스트가 비어있으면 비교할 대상이 없으므로 비교하지 않고 바로 리스트에 추가한다.)

비교 결과에 따라서 리스트에 n이 들어가는 위치가 달라진다.

 

① list.get(list.size()-1) 가 n 보다 작으면, 리스트의 마지막에 n을 추가한다.

 

② list.get(list.size()-1) 가 n 보다 크면, 이분탐색을 진행하여 n 이 들어갈 위치를 찾는다. 그리고 해당 위치의 값을

    n으로 대체한다.

 

위 과정을 수열의 마지막 요소까지 반복한다.

 

 

이해를 돕기 위해 예제를 살펴보자.

 

 

[예제]

주어진 수열이 10 20 1 2 3 4 8 6 일 때, 이 수열에서 최장 증가 수열을 구하라.

 

1. 리스트가 비어있으므로 첫 번째 요소를 리스트에 추가한다. list.add(10)

 

 

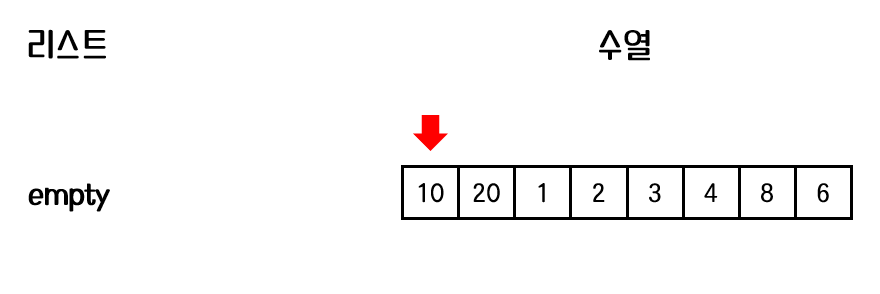
2. 리스트의 가장 마지막 원소는 10 이다. 10과 비교했을 때 20이 더 크므로 리스트의 마지막에 20을 추가한다. 

   list.add(20)

   (분홍색은 업데이트된 요소, 하늘색은 기존의 요소를 의미)

 

3. 리스트의 가장 마지막 원소는 20 이다. 20과 비교했을 때 1이 더 작으므로 이분탐색을 진행한다.

   리스트가 오름차순을 유지해야 하므로 1이 들어갈 위치는 리스트의 0번째 자리이다. 

   이 때 주의해야 할 것은 10 보다 앞에 1을 추가하는 것이 아니라, 10을 1로 대체해야 한다.

   list.set(0,1)

 

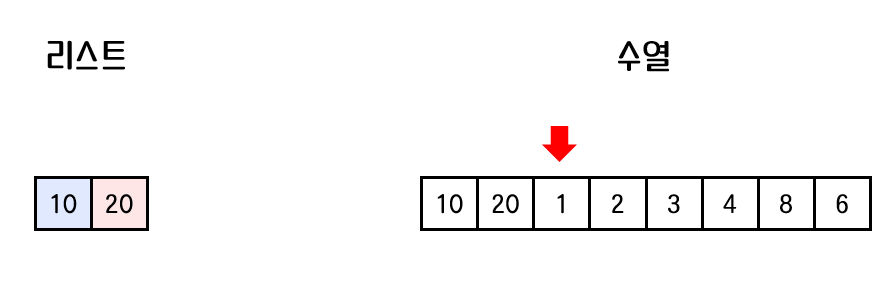
4. 리스트의 마지막 원소는 20 이다. 20과 비교했을 때, 2가 더 작으므로 이분탐색을 진행한다.

   2는 1보다 크고, 20 보다 작으므로 2가 들어가야 하는 위치는 리스트의 1번째 자리이다.

   역시 마찬가지로 20 대신에 2로 대체된다. list.set(1,2)

 

5. 2과 비교했을 때, 3이 더 크므로 리스트의 마지막에 3을 추가한다. list.add(3)

 

6. 이제 리스트의 마지막 요소는 3이다. 3과 비교했을 때 4가 더 크므로 리스트의 마지막에 4를 추가한다. list.add(4)

 

7. 리스트의 마지막 요소는 4이다. 4와 비교했을 때, 8이 더 크므로 리스트의 마지막에 8을 추가한다. list.add(8)

 

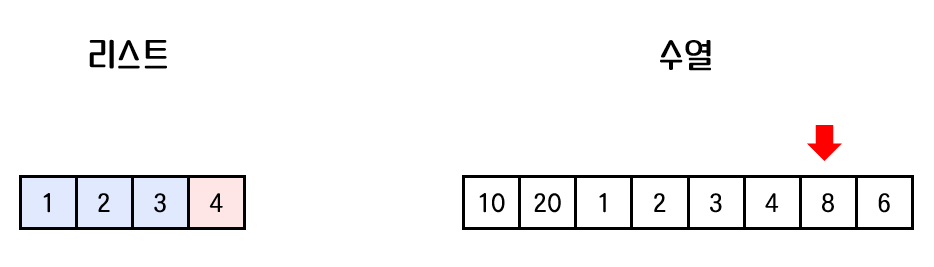
8. 리스트의 마지막 요소 8과 비교했을 때, 6이 더 작으므로 이분탐색을 진행한다.

   6은 4보다 크고 8보다 작으므로 6이 들어갈 위치는 4번째이다. 그러므로 8이 6으로 대체된다. list.set(4,6)

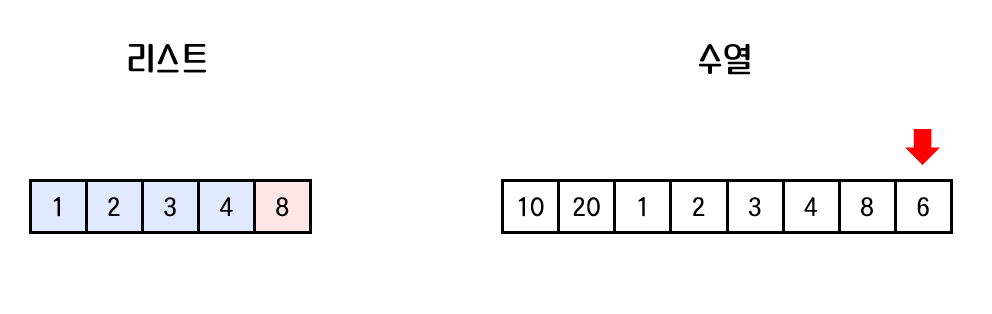
최종 리스트는 아래와 같다. 즉, 최종적으로 가장 긴 증가하는 수열의 길이는 5가 된다.

list.size() = 5

 

소스코드 : 

다음은 백준 12015번 '가장 긴 증가하는 부분 수열 2' 의 소스코드이다.