LIS(Lowest Increasing Subsequence) - 수열 구하기

저번 글에서는 최장 증가 수열의 길이를 구하는 경우에 대해 다루었다.

 

LIS(Lowest Increasing Subsequence) - 길이 구하기

이분탐색을 이용하여서 새로 입력받은 수가 리스트에 들어갈 위치를 구하였다.

그러나 이 알고리즘은 최장 증가 수열의 길이를 구할 수는 있지만 수열 자체를 구할 수는 없었다.

(위의 포스팅 참고)

 

예를 들어, 다음과 같은 반례가 있다.

수열 10 30 50 20 60 이 있다고 할 때 위의 알고리즘을 사용하면 최종적으로 리스트에 남아있는

수는 10 20 50 60 이 된다. 리스트의 크기는 4개로, 이는 최장 증가 부분수열의 길이에 해당하지만, 리스트에 남아 있는 10 20 50 60 자체는 최장 증가 부분수열이 아니다.

 

따라서 최장 증가 부분수열 자체를 구하기 위해서는 위 알고리즘에서 추가적으로 역추적하는 과정이 필요하다.

역추적을 하기 위해서 Pair 객체를 가지는 track이라는 배열을 추가하였다.

Pair[] track = new Pair[N];

 

Pair는 입력받은 수(n)와 이 입력받은 수가 리스트의 어디에 들어가는지 그 인덱스(idx)를 가지고 있다.

 class Pair {

	 int n, idx;

	 Pair(int n, int idx) {
	   	 this.n = n;
		 this.idx = idx;
	 }
 }

 

입력받은 수를 리스트의 알맞은 위치(idx)에 넣은 후(여기까지는 이전 글에서의 알고리즘과 동일하다.)

이 track이라는 배열에 Pair(n, idx) 객체를 생성하여 넣어준다.

 

수정된 코드 : 

코드에 대한 자세한 설명은 이전 LIS(최장 증가 수열) 글에서 확인할 수 있다.

 for (int i = 0; i < N; i++) {
	 int n = Integer.parseInt(sarr[i]);

	 if (list.size() == 0 || list.get(list.size() - 1) < n) {
		 list.add(n);
		 track[i] = new Pair(n, list.size() - 1);
	 } else {
		 int idx = binSearch(n, 0, list.size() - 1);
		 list.set(idx, n);
		 track[i] = new Pair(n, idx);
	 }
 }

입력받은 수열이 차례대로 10 30 50 20 60 일 때, 최종적으로 리스트에 남아있는 수와 track 배열은 다음과 같이 된다.

 

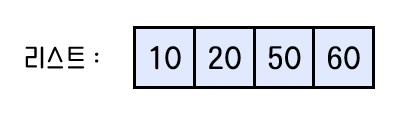
track[0] = new Pair(10, 0)

track[1] = new Pair(30, 1)

track[2] = new Pair(50, 2)

track[3] = new Pair(20, 1)

track[4] = new Pair(60, 3)

 

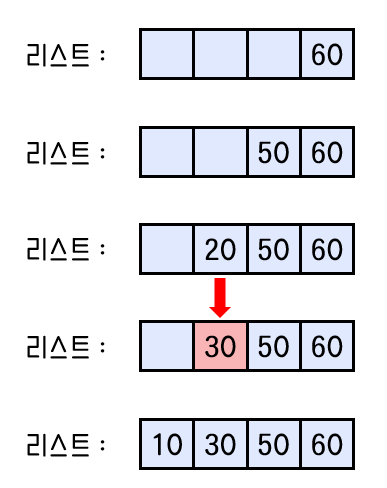
i = 4부터 i = 0 까지 idx가 3부터(리스트의 마지막 요소의 위치가 3이므로)

하나씩 감소하며 해당 idx를 가지는 n을 찾는다.

 int idx = list.size() - 1;
 for (int i = N - 1; i >= 0; i--) {
	 if (track[i].idx == idx) {
		 list.set(idx, track[i].n);
		 idx--;
	 }
 }

 

전체 소스코드는 다음과 같다.

백준 14003번 : 가장 긴 증가하는 부분 수열 5 의 소스코드이다.