그래프 탐색에는 두 가지 방법이 있다.
- DFS(Depth First Search)
- BFS(Breadth First Search)
DFS 는 이름 그대로 깊이를 우선시 하여 탐색하는 방법이다. '한 우물만 판다' 라는 느낌처럼 한 길만 계속 깊이 파고드는 방식이다.
반면에 BFS 는 넓이를 우선시한다. 특정 노드와 연결된 모든 노드를 한번씩 거친 다음에 다음 노드로 이동하는 방식이다.
예를 들어, 다음과 같은 그래프가 있고 1번부터 탐색을 시작한다고 할 때

왼쪽과 같은 탐색 방법을 DFS, 오른쪽과 같은 탐색 방법을 BFS라고 할 수 있다.
DFS : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5
BFS : 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7


위의 DFS 방식에서 처음에 꼭 1 -> 2 로 가는 방법만 있는 것은 아니다.
1 -> 3 으로 가도 되고, 그 다음도 마찬가지로 2 ->4 가 아니라 2-> 5 로 가는 방법도 존재한다.
중요한 것은 연결된 노드 중 어디로 가느냐가 아니라 계속 깊이 파고드는 모양새를 하면서 탐색을 진행한다는 점이다. 특정 노드와 연결된 다른 노드들을 찾으면 그 중에 하나를 골라 이동하고, 다시 또 그와 연결된 노드들 중 하나를 골라 이동하는 방식이 반복된다.
만약 현재 노드에서 더 이상 이동할 노드가 없다면, 이전 노드로 되돌아간다.(<- 백트래킹)
반면, BFS는 특정 노드와 연결된 노드가 여러개 있다면 몇개가 되었든 우선 모두 다 탐색을 한다.
1번 노드와 연결된 노드가 2번 3번일 때, DFS는 2번을 탐색한 후에 3번을 탐색하지 않고 바로 4번으로 이동했다면, BFS는 2번도 탐색하고 3번도 탐색한 후에 4번으로 이동한다.
이번 글에서는 두 가지 그래프 탐색 중 DFS를 어떻게 구현할 수 있을지 알아보자.
DFS는 스택의 방식과 매우 유사하다.
DFS는 스택을 이용하여 구현할 수 있다.
위의 그래프의 DFS 진행 방식을 스택과 비교하여 천천히 살펴보자.
노드를 탐색할 때마다 해당 노드를 스택에 push 할 것이다.
먼저 그래프 탐색을 1번에서 시작할 때, 1번은 탐색이 완료되었으므로 스택에 1번을 push 한다.
탐색 순서 : 1

그 다음 1번 노드와 연결된 노드는 2번과 3번이 있다. 이 두 곳 중 하나를 선택하여 이동할 수 있다.
여기서는 2번을 선택했다고 가정하자. 그러면 2번 노드를 탐색한 것이므로 스택에 2번 노드를 push 한다.
탐색 순서 : 1 -> 2

2번 노드와 연결된 노드는 4번과 5번이다.
4번을 선택하여 이동한다고 하면, 스택에 4번 노드를 push 한다.
탐색 순서 : 1 -> 2 -> 4

4번 노드와 연결된 노드는 5번과 7번이다.
7번 노드를 선택하여 이동한다고 하면, 스택에 7번 노드를 push 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7

7번 노드와 연결된 노드는 5번과 6번이다.
6번 노드를 선택하여 이동한다고 하면, 스택에 6번 노드를 push 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6

6번 노드와 연결된 노드는 3번 노드이다.
3번 노드로 이동해야 하므로 스택에 3번 노드를 push 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3

3번 노드와 연결된 노드는 1번과 5번이다.
1번은 이미 방문했으므로 고려하면 안된다. 그러므로 나머지 하나인 5번 노드로 이동한다.
스택에 5번 노드를 push 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5

5번 노드와 연결된 노드는 2번, 3번, 4번, 6번, 7번 노드이다.
그런데 5개의 노드 모두 이미 탐색이 완료되었으므로 다시 방문해서는 안된다.
이렇게 현재 노드와 연결된 노드들 중 이동할 노드가 하나도 없다면, 다시 전 단계의 노드로 되돌아가야 한다. 이렇게 되돌아 가는 행위는 스택에서의 pop과 유사하다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5

3번 노드로 되돌아왔다. 이제 3번 노드와 연결된 노드들 중 아직 방문하지 않은 노드가 있는지 본다.
3번과 연결된 1번, 6번 노드 모두 이미 탐색이 완료된 상태이다.
3번 노드 역시 더 이상 이동할 노드가 없으므로 다시 전 단계인 6번으로 되돌아 가야한다.
스택에서는 3번 노드를 pop 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5

6번 노드로 되돌아왔다. 6번 노드와 연결된 노드들 중 아직 방문하지 않은 노드가 있는지 본다.
6번과 연결된 다른 노드 모두 이미 탐색이 완료된 상태이다.
더 이상 이동할 노드가 없으므로 6번의 전 단계인 7번으로 되돌아 가기 때문에 스택에서 6번 노드를 pop 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5
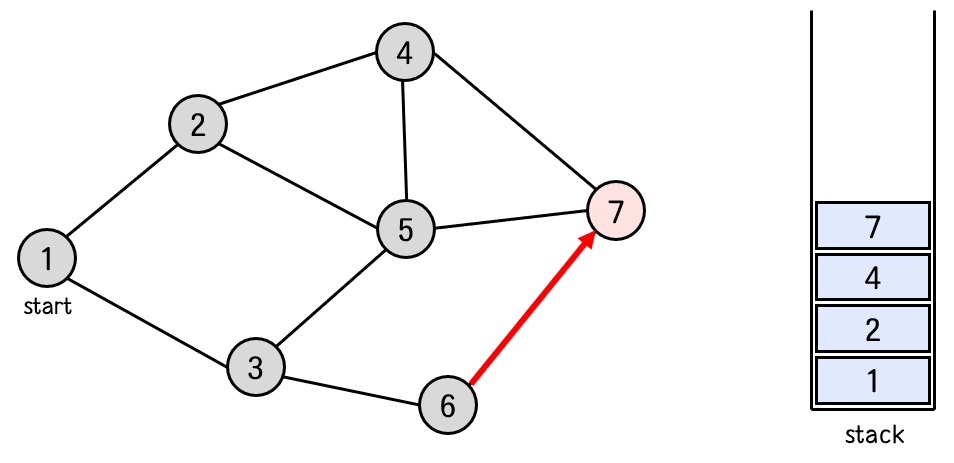
7번 노드로 되돌아왔다. 7번 노드와 연결된 노드들 중 아직 방문하지 않은 노드가 없다.
더 이상 이동할 노드가 없으므로 7번의 전 단계인 4번으로 되돌아간다.
역시 스택에서 7번 노드를 pop 해준다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5

4번 노드와 연결된 노드들 중 아직 방문하지 않은 노드가 없다.
더 이상 이동할 노드가 없으므로 전 단계인 2번 노드로 되돌아간다.
스택에서 4번 노드를 pop 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5
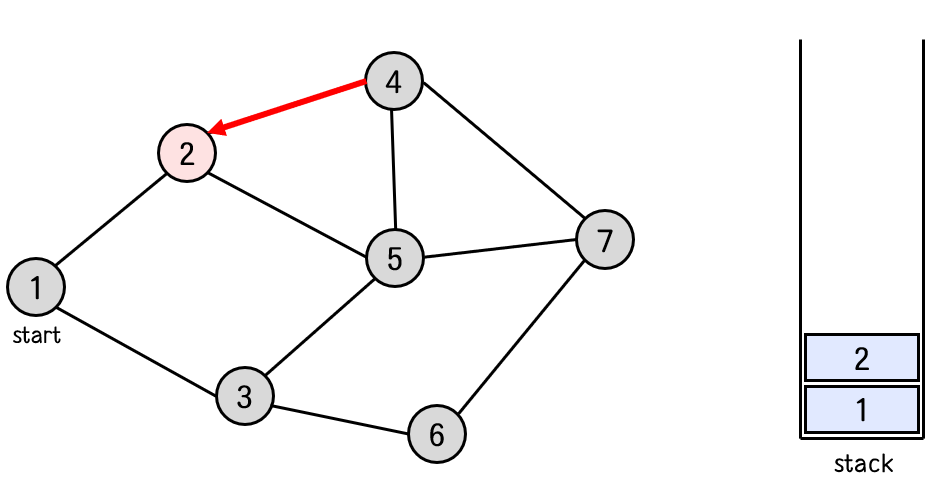
2번 노드와 연결된 노드들 중 아직 방문하지 않은 노드가 없다.
더 이상 새롭게 이동할 노드가 없기 때문에 2번 노드의 전 단계였던 1번 노드로 되돌아간다.
스택에서 2번 노드를 pop 한다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5

마지막 1번 노드 역시 1번 노드와 연결된 노드들 중에 아직 방문하지 않은 노드가 없기 때문에
스택에서 pop을 해준다. 마지막 1번 노드를 pop 함으로써 스택은 비어있게 된다.
즉, 스택이 비어있게 되면 DFS 방식의 그래프 탐색이 종료된다.
탐색 순서 : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5

스택을 이용한 소스코드 :
public static void dfs() {
Stack<Integer> stack = new Stack<>();
stack.push(V); // 시작 노드 push
visited[V] = true; // 시작 노드를 방문처리
while (!stack.isEmpty()) {
int n = stack.peek();
boolean flag = false; // 연결된 노드 중 아직 방문하지 않은 노드가 있는지 알기 위해서
for (int node : v[n]) {
if (!visited[node]) { // 노드 n과 연결된 노드 node가 아직 방문하지 않은 상태라면
stack.push(node); // 스택에 push 한다.
visited[node] = true; // 방문처리
flag = true;
break;
}
}
if (!flag) // 방문하지 않은 노드가 하나도 없다면
stack.pop(); // 노드 n을 스택에서 pop
}
}
DFS를 재귀로도 구현할 수 있다.
스택과 재귀는 그 진행 방식이 흡사하다. 아래는 재귀를 이용하여 dfs를 구현한 코드이다.
스택을 이용한 코드보다 간결해졌다.
재귀를 이용한 소스코드 :
public static void dfs(int n) {
visited[n] = true;
for (int node : v[n]) {
if (!visited[node]) {
dfs(node);
}
}
}
DFS 시간복잡도
dfs의 시간복잡도는 그래프 정점간의 연결 관계를 인접 리스트로 하느냐, 인접 행렬로 하느냐에 따라 달라진다. 여기서는 그래프의 연결관계에 대한 설명은 생략한다.
그래프 연결관계 - 인접 행렬, 인접 리스트
그래프 관련하여 문제를 풀다보면(가령 DFS, BFS 문제와 같은) 그래프에서 노드간의 연결관계를 저장해야 하는 경우가 있다. 이럴 때 그래프의 연결관계를 표현하는 방법이 대표적으로 두 가지가
lotuslee.tistory.com
정점의 개수를 V, 간선의 개수를 E 라고 할 때
인접 행렬을 사용할 경우 시간복잡도 : O(V²)
노드 n의 인접 노드를 찾는 과정에서 O(V)의 시간복잡도가 필요하고, 모든 정점을 탐색해야하므로 V번 반복해야 하기 때문에 총 시간 복잡도는 O(V²) 가 된다.
인접 리스트를 사용할 경우 시간복잡도 : O(V+E)
노드 n의 리스트에는 노드 n과 인접한 노드 개수만큼만(차수만큼) 들어있다. 다른 노드의 경우도 이러할 것이다. 이 개수를 모두 합하면 결국에는 간선의 개수인 E가 된다. 그리고 모든 정점을 탐색할 때 V번 반복하므로 총 시간 복잡도는 O(V+E)이다.
DFS 장단점
[장점]
- 메모리가 적게 든다. DFS를 사용하면 깊이만큼의 공간만 필요하다. 위의 예제에서 스택에 가장 높이 쌓일 때는 정점을 모두 방문했을 때인 V 만큼이다. 즉, 이동한 경로상에 있는 정점만큼의 크기만 필요하기 때문에 BFS보다 메모리가 적게 든다는 장점이 있다.
- 찾으려는 노드가 깊은 곳에 있다면 DFS 방식이 유리하다.
[단점]
- 소위 삽질할 수 있다. 한 우물만 팠는데 우물을 잘못 판 것이다. DFS 방식으로 탐색했는데 끝내 원하는 노드를 찾지 못하는 경우가 이에 해당한다. 그러면 백트래킹으로 다시 빠져나와 다른 경로를 탐색해야 한다. 즉, 효율성이 떨어진다.
'Algorithm & DS > 그래프' 카테고리의 다른 글
| 플로이드 워셜(Floyd - Warshall) (0) | 2021.03.10 |
|---|---|
| BFS(Breadth First Search) - 너비 우선 탐색 (0) | 2021.02.25 |
| MST(Minimum Spanning Tree) - 1. 프림 알고리즘 (0) | 2021.02.23 |
| 다익스트라(Dijkstra) (0) | 2021.02.13 |
| 그래프 연결관계 - 인접 행렬, 인접 리스트 (0) | 2020.01.05 |