그래프 탐색에는 두 가지 방법이 있다.
- DFS(Depth First Search)
- BFS(Breadth First Search)
이번에는 BFS에 대해서 다뤄볼 것이다.
DFS(Depth First Search) - 깊이 우선 탐색
그래프 탐색에는 두 가지 방법이 있다. DFS(Depth First Search) BFS(Breadth First Search) DFS 는 이름 그대로 깊이를 우선시 하여 탐색하는 방법이다. '한 우물만 판다' 라는 느낌처럼 한 길만 계속 깊이..
lotuslee.tistory.com
BFS는 너비 우선 탐색으로 특정 노드와 연결된 모든 노드들을 우선적으로 탐색한 뒤, 그 중에 하나를 선택하여 또 다시 그와 연결된 모든 노드들을 탐색하는 방식으로 진행된다. 하나의 경로만을 깊이있게 탐색하는 방법인 DFS와 달리 모든 노드를 한번씩 거치면서 이동하기 때문에 너비 우선 탐색이라는 이름이 붙여졌다.


BFS는 큐를 이용하여 구현한다.
BFS는 큐를 이용하여 구현할 수 있다.
그래프에서 1번 정점을 시작정점으로 하자.
먼저 1번 노드를 방문처리하고 큐에 1번 노드를 넣는다.
탐색 순서 : 1
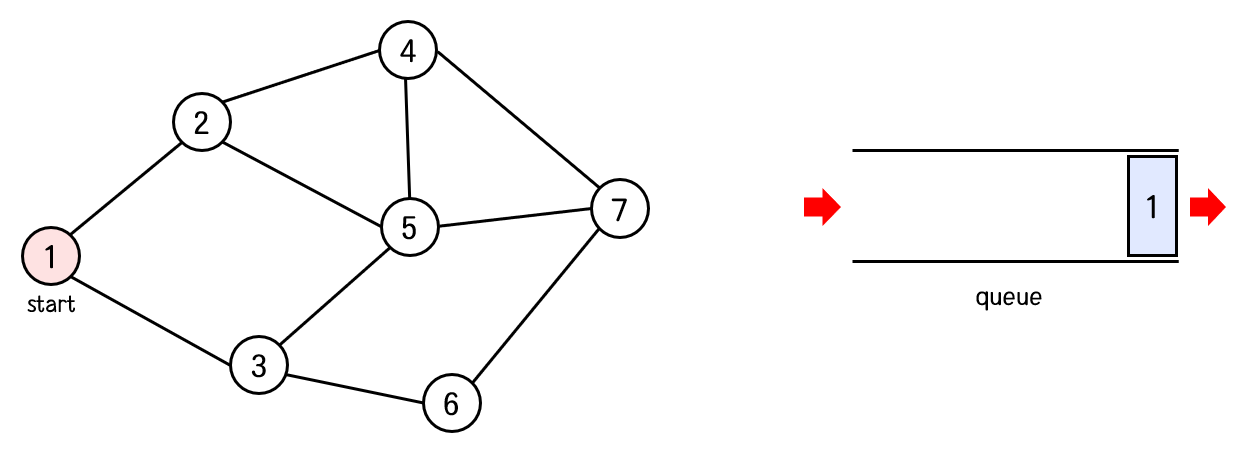
이제 큐의 front에 있는 1번 노드를 poll 한다.
1번 정점과 연결된 정점 중 아직 방문하지 않은 정점은 2번과 3번이다.
그러므로 2번과 3번을 방문처리하고, 두 정점을 차례대로 큐에 넣어주면 다음과 같다.
탐색 순서 : 1

다시 큐에서 front에 있는 2번 정점을 꺼낸다.
이제 2번 정점과 연결 되며, 아직 방문하지 않은 정점을 찾으면 4번과 5번이 된다.
4번, 5번 정점을 방문처리하고, 두 정점을 큐에 넣어준다.
탐색 순서 : 1 -> 2

큐의 front에서 3번 정점을 꺼낸다.
3번 정점과 연결된 노드 중 방문하지 않은 노드는 6번 노드이다.
따라서 6번 노드를 방문처리하고, 큐에 넣어준다.
탐색 순서 : 1 -> 2 -> 3

큐의 front에서 4번 노드를 꺼낸다.
4번 노드와 연결된 노드 중 방문하지 않은 노드는 7번 노드이다.
따라서 7번 노드를 방문처리하고, 큐에 넣어준다.
탐색 순서 : 1 -> 2 -> 3 -> 4
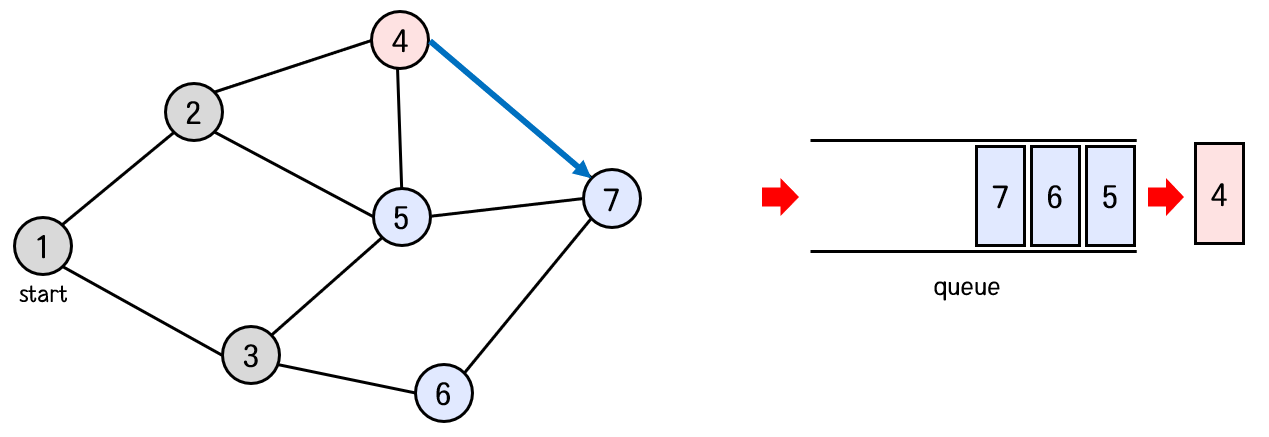
큐의 front에서 5번 노드를 꺼낸다.
5번 노드와 연결된 노드 중 방문하지 않은 노드가 하나도 없다.
그러므로 새로 큐에 들어가는 노드는 없다.
탐색 순서 : 1 -> 2 -> 3 -> 4 -> 5

큐의 front에서 6번 노드를 꺼낸다.
6번 노드와 연결된 노드 중 방문하지 않은 노드가 하나도 없으므로 역시 새로 큐에 들어가는 노드는 없다.
탐색 순서 : 1 -> 2 -> 3 -> 4 -> 5 -> 6
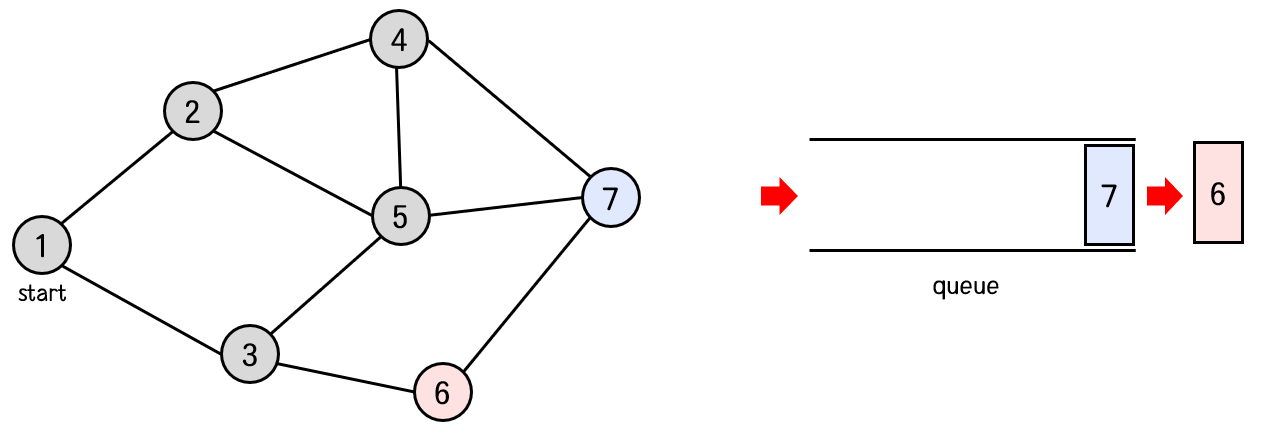
큐의 front에서 7번 노드를 꺼낸다.
7번 노드와 연결된 노드 중 아직 방문하지 않은 노드는 없으므로 새롭게 큐에 들어가는 노드는 없다.
그러므로 큐는 비어있게 된다.
탐색 순서 : 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7

큐가 비어있으므로 탐색을 종료한다.
큐를 이용한 소스코드 :
public static void bfs() {
Queue<Integer> q = new LinkedList<>();
q.offer(V); // 시작 정점을 큐에 넣음
visited[V] = true; // 시작 정점을 방문 처리
while (!q.isEmpty()) {
int n = q.poll(); // 큐에서 꺼낸다.
for (int node : v[n]) {
if (!visited[node]) { // 연결된 노드가 아직 방문전이면
q.offer(node); // 큐에 해당 노드를 넣고
visited[node] = true; // 방문처리한다.
}
}
}
}
BFS 시간복잡도
정점의 개수를 V, 간선의 개수를 E 라고 할 때
인접 행렬을 사용할 경우 시간복잡도 : O(V²)
노드 n의 인접 노드를 찾는 과정에서 O(V)의 시간복잡도가 필요하고, 모든 정점을 탐색해야하므로 V번 반복해야 하기 때문에 총 시간 복잡도는 O(V²) 가 된다.
인접 리스트를 사용할 경우 시간복잡도 : O(V+E)
노드 n의 리스트에는 노드 n과 인접한 노드 개수만큼만(차수만큼) 들어있다. 다른 노드의 경우도 이러할 것이다. 이 개수를 모두 합하면 결국에는 간선의 개수인 E가 된다. 그리고 모든 정점을 탐색할 때 V번 반복하므로 총 시간 복잡도는 O(V+E)이다.
BFS 장단점
[장점]
- 최단 거리를 찾는 문제에 적합하다.
예를 들어, 위의 예시에서 설명했던 그래프에서 1번 노드에서 5번 노드까지 가는 최단 경로를
찾는다고 하자.

DFS로 최단경로를 찾는다고 하면,
5번 노드에 도착했을 때, 1-> 2 -> 4 -> 5 경로를 통해 도달했을 수도 있다.
혹은, 더 돌아가서 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5 경로를 통해 도달했을 수도 있다.
이렇게 DFS 방식으로 최단경로를 찾으면 해당 노드에 도착했다 하더라도 최단경로로 도착했다는
것이 보장되지 않으므로 여러번의 시행착오를 거쳐가며 최단경로인지 아닌지를 확인한다.
하지만 BFS로 최단경로를 찾으면,
1번노드에서 시작할 때, 1번과 연결된 2번,3번 노드를 모두 방문하고, 그 다음에 2번 노드와 연결된
4번, 5번 노드를 방문하게 된다.
BFS로 탐색하여 5번 노드에 도착했을 때,
1(이동거리 0) -> 2(이동거리 1) -> 3(이동거리 1) -> 4(이동거리 2) -> 5(이동거리 2)
최단 거리를 갖는 경로로 5번 노드에 도착하기 때문에 바로 최단경로를 알아낼 수 있다.
- 깊이가 얕은 그래프일 경우에 유용하다.
[단점]
- 메모리 사용이 크다. DFS에서 스택을 사용할 때는 현재 경로상에 있는 노드들만 스택에 저장하였다. 하지만 BFS에서는 다음에 탐색할 노드까지 큐에 저장해두기 때문에 DFS에 비해 공간을 많이 사용한다. 예를 들어, 1번 노드에서 인접한 2번, 3번 노드를 모두 큐에 저장해둔다. 그리고 2번 노드와 인접한 노드를 찾는 동안에 3번 노드는 큐에서 대기하고 있다.
'Algorithm & DS > 그래프' 카테고리의 다른 글
| 플로이드 워셜(Floyd - Warshall) (0) | 2021.03.10 |
|---|---|
| DFS(Depth First Search) - 깊이 우선 탐색 (0) | 2021.02.24 |
| MST(Minimum Spanning Tree) - 1. 프림 알고리즘 (0) | 2021.02.23 |
| 다익스트라(Dijkstra) (0) | 2021.02.13 |
| 그래프 연결관계 - 인접 행렬, 인접 리스트 (0) | 2020.01.05 |