신장 트리(Spanning Tree)
: 모든 정점이 간선으로 연결되어 있으면서 사이클이 없는 그래프
예를 들어, 다음과 같은 그래프가 있다고 하자.
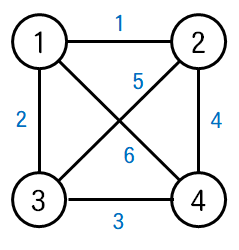
위 그래프에서 가능한 신장 트리는 아래와 같다.
1번부터 4번까지의 모든 정점이 연결되있으면서 사이클이 존재하지 않는다.

아래의 경우는 신장 트리가 아니다.
모든 정점이 연결되어 있으나 사이클이 존재하기 때문이다.

MST(Minimum Spanning Tree)
신장 트리 중에서 간선의 비용(가중치)의 합이 최소가 되는 것을 최소 신장 트리라고 한다.
위의 그래프에서 6개의 신장 트리 중에 최소 신장 트리는 간선의 비용의 합이 6이 되는 경우이다.

MST를 구하는 알고리즘은 대표적으로 2가지가 있다.
1. 프림(Prim) 알고리즘
2. 크루스칼(Kruskal) 알고리즘
이번에는 프림(Prim) 알고리즘에 대해 먼저 공부할 것이다.
프림(Prim) 알고리즘
프림 알고리즘은 노드를 중심으로 간선을 탐색하는 방법이다.
시간복잡도 : O(ElogV)
알고리즘 :
1. 임의의 start 정점을 하나 선택하여 우선순위 큐에 넣는다.
2. 우선순위 큐에서 정점을 하나 꺼낸다.
(우선순위에 의해 비용이 가장 작은 정점이 우선순위 큐를 빠져나온다.)
3. 우선순위 큐에서 꺼낸 정점이 이미 방문한 정점이라면, 다시 우선순위 큐에서 새로운 정점을 꺼낸다.
4. 우선순위 큐에서 꺼낸 정점이 아직 방문하지 않은 정점이라면, 방문처리를 하고 정점의 비용을 더한다.
5. 위의 정점과 연결된 다른 정점들 중 방문하지 않은 정점들의 정보를 우선순위 큐에 넣음
6. 우선순위 큐가 비어있을 때까지 2~5번 과정을 반복
[예제]
다음과 같은 그래프가 있을 때 프림 알고리즘을 이용하여 최소 신장 트리를 구하는 방법을 알아보자.

우선 시작(start) 정점을 하나 정해야 한다. 시작 정점을 1번이라고 정하자.
우선순위 큐에 1번 정점의 정보를 넣는다. 처음에 시작 정점의 간선 비용은 0으로 설정한다.
우선순위 큐에는 (정점 번호(N) = 1, 비용(W) = 0) 의 정보가 들어가게 된다.
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점이 꺼내진다.
(여기서는 우선순위 큐에 정점 1번 하나만 존재하므로 정점 1번이 꺼내진다.)
2. 우선순위 큐에서 나온 1번 정점을 방문처리 한다. -> visited[1] = true3. 그리고 간선 비용의 총 합을 구하는 변수 sum에 정점 1번의 비용인 0을 더한다. -> sum = 04. 정점 1번과 연결된 정점은 2번과 3번이다. 그러므로 2번, 3번 정점을 우선순위 큐에 넣는다.
(정점 번호(N) = 2, 1번과 2번 사이 간선 비용(W) = 10), (정점 번호(N) = 3, 1번과 3번 사이 간선 비용(W) = 4)
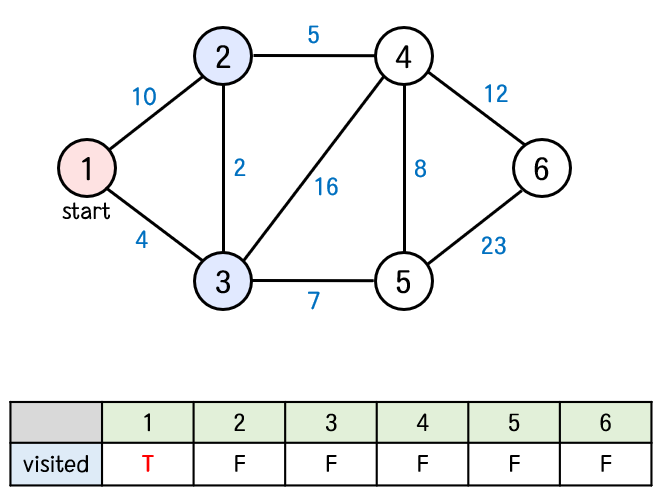
우선순위 큐 : (N = 2, W = 10), (N = 3, W = 4)
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점인 (N = 3, W = 4)이 꺼내진다.
2. 3번 정점을 방문처리 한다. -> visited[3] = true
3. 간선 비용의 총 합을 구하는 변수 sum에 정점 3번의 비용인 4를 더한다. -> sum = 4
4. 정점 3번과 연결된 정점은 1번, 2번, 4번, 5번이다.
1번은 이미 방문되었으므로 2,3,5번의 정점을 우선순위 큐에 넣는다.

우선순위 큐 : (N = 2, W = 10), (N = 2, W = 2), (N = 4, W = 16), (N = 5, W = 7)
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점인 (N = 2, W = 2)이 꺼내진다.
2. 2번 정점을 방문처리 한다. -> visited[2] = true
3. 간선 비용의 총 합을 구하는 변수 sum에 비용 2를 더한다. -> sum = 6
4. 정점 2번과 연결된 정점 중 아직 방문하지 않은 정점은 4번이다.
4번 정점을 우선순위 큐에 넣는다.

우선순위 큐 : (N = 2, W = 10), (N = 4, W = 16), (N = 5, W = 7), (N = 4, W = 5)
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점인 (N = 4, W = 5)이 꺼내진다.
2. 4번 정점을 방문처리 한다. -> visited[4] = true
3. 간선 비용의 총 합을 구하는 변수 sum에 비용 5를 더한다. -> sum = 11
4. 정점 4번과 연결된 정점 중 아직 방문하지 않은 정점은 5,6번이다.
5번, 6번 정점을 우선순위 큐에 넣는다.

우선순위 큐 : (N = 2, W = 10), (N = 4, W = 16), (N = 5, W = 7), (N = 5, W = 8), (N = 6, W = 12)
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점인 (N = 5, W = 7)이 꺼내진다.
2. 5번 정점을 방문처리 한다. -> visited[5] = true
3. 간선 비용의 총 합을 구하는 변수 sum에 비용 7를 더한다. -> sum = 18
4. 정점 5번과 연결된 정점 중 아직 방문하지 않은 정점은 6번이다.
6번 정점을 우선순위 큐에 넣는다.

우선순위 큐 : (N = 2, W = 10), (N = 4, W = 16), (N = 5, W = 8), (N = 6, W = 12), (N = 6, W = 23)
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점인 (N = 5, W = 8)이 꺼내진다.
2. 그런데 5번 정점은 이미 방문이 완료된 상태이다.
그러므로 다시 우선순위 큐에서 새로 꺼내야 한다.
우선순위 큐 : (N = 2, W = 10), (N = 4, W = 16), (N = 6, W = 12), (N = 6, W = 23)
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점인 (N = 2, W = 10)이 꺼내진다.
2. 이번에도 역시 2번 정점은 이미 방문이 완료된 상태이므로 다시 우선순위 큐에서 꺼낸다.
우선순위 큐 : (N = 4, W = 16), (N = 6, W = 12), (N = 6, W = 23)
1. 우선순위 큐에서 정점 하나를 꺼낸다.
우선순위에 따라 우선순위 큐에 있는 정점들 중 비용이 가장 작은 정점인 (N = 6, W = 12)이 꺼내진다.
2. 6번 정점은 아직 방문하지 않은 상태다. 그러므로 6번 정점을 방문처리 한다. -> visited[6] = true
3. 간선 비용의 총 합을 구하는 변수 sum에 비용 12를 더한다. -> sum = 30
4. 정점 6번과 연결된 정점 중 아직 방문하지 않은 정점은 없다.
그러므로 우선순위 큐에 새롭게 들어가는 정점은 없다.

우선순위 큐 : (N = 4, W = 16), (N = 6, W = 23)
아직 우선순위 큐가 비어있지 않지만 하나씩 꺼내었을 때, 이미 모든 정점이 방문이 완료된 상태이므로 아무 작업도 하지 않고 끝나게 된다.
모든 정점을 방문하였으므로 sum 에 들어있는 값이 최종 최소 신장 트리의 간선 비용 합이 된다.
그리고 최소 신장 트리는 아래와 같다.

최소 간선 트리의 비용의 합 : sum = 4 + 2 + 5 + 7 + 12 = 30
소스코드 :
public static long getMST() {
PriorityQueue<Pair> pq = new PriorityQueue<>();
long sum = 0;
pq.offer(new Pair(1, 0));
while (!pq.isEmpty()) {
Pair pair = pq.poll();
if (visited[pair.n])
continue;
visited[pair.n] = true;
sum += pair.w;
for (Pair np : arr[pair.n]) {
if (!visited[np.n])
pq.offer(np);
}
}
return sum;
}
static class Pair implements Comparable<Pair> {
int n, w;
Pair(int n, int w) {
this.n = n;
this.w = w;
}
@Override
public int compareTo(Pair o) {
return w - o.w;
}
}
'Algorithm & DS > 그래프' 카테고리의 다른 글
| 플로이드 워셜(Floyd - Warshall) (0) | 2021.03.10 |
|---|---|
| BFS(Breadth First Search) - 너비 우선 탐색 (0) | 2021.02.25 |
| DFS(Depth First Search) - 깊이 우선 탐색 (0) | 2021.02.24 |
| 다익스트라(Dijkstra) (0) | 2021.02.13 |
| 그래프 연결관계 - 인접 행렬, 인접 리스트 (0) | 2020.01.05 |