SY DevLog

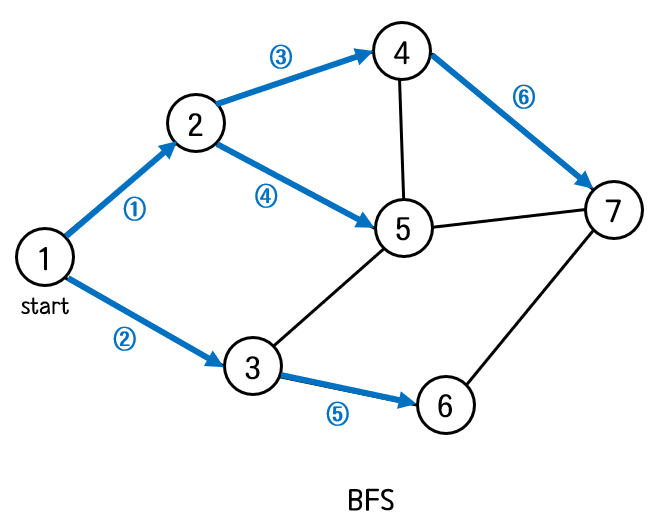
그래프 탐색에는 두 가지 방법이 있다. DFS(Depth First Search) BFS(Breadth First Search) 이번에는 BFS에 대해서 다뤄볼 것이다. DFS(Depth First Search) - 깊이 우선 탐색 그래프 탐색에는 두 가지 방법이 있다. DFS(Depth First Search) BFS(Breadth First Search) DFS 는 이름 그대로 깊이를 우선시 하여 탐색하는 방법이다. '한 우물만 판다' 라는 느낌처럼 한 길만 계속 깊이.. lotuslee.tistory.com BFS는 너비 우선 탐색으로 특정 노드와 연결된 모든 노드들을 우선적으로 탐색한 뒤, 그 중에 하나를 선택하여 또 다시 그와 연결된 모든 노드들을 탐색하는 방식으로 진행된다. 하나의 경로만을 깊..

그래프 탐색에는 두 가지 방법이 있다. DFS(Depth First Search) BFS(Breadth First Search) DFS 는 이름 그대로 깊이를 우선시 하여 탐색하는 방법이다. '한 우물만 판다' 라는 느낌처럼 한 길만 계속 깊이 파고드는 방식이다. 반면에 BFS 는 넓이를 우선시한다. 특정 노드와 연결된 모든 노드를 한번씩 거친 다음에 다음 노드로 이동하는 방식이다. 예를 들어, 다음과 같은 그래프가 있고 1번부터 탐색을 시작한다고 할 때 왼쪽과 같은 탐색 방법을 DFS, 오른쪽과 같은 탐색 방법을 BFS라고 할 수 있다. DFS : 1 -> 2 -> 4 -> 7 -> 6 -> 3 -> 5 BFS : 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 위의 DFS 방식에서 처음에 꼭..

신장 트리(Spanning Tree) : 모든 정점이 간선으로 연결되어 있으면서 사이클이 없는 그래프 예를 들어, 다음과 같은 그래프가 있다고 하자. 위 그래프에서 가능한 신장 트리는 아래와 같다. 1번부터 4번까지의 모든 정점이 연결되있으면서 사이클이 존재하지 않는다. 아래의 경우는 신장 트리가 아니다. 모든 정점이 연결되어 있으나 사이클이 존재하기 때문이다. MST(Minimum Spanning Tree) 신장 트리 중에서 간선의 비용(가중치)의 합이 최소가 되는 것을 최소 신장 트리라고 한다. 위의 그래프에서 6개의 신장 트리 중에 최소 신장 트리는 간선의 비용의 합이 6이 되는 경우이다. MST를 구하는 알고리즘은 대표적으로 2가지가 있다. 1. 프림(Prim) 알고리즘 2. 크루스칼(Kruska..

힙 정렬(Heap Sort) 힙(heap)을 이용하는 정렬 알고리즘 힙(heap) : 부모 노드의 값이 자식 노드의 값보다 큰 완전이진트리 부모 노드의 값이 자식 노드의 값보다 항상 크기 때문에 힙의 루트에는 제일 큰 수가 들어가게 된다. 이를 이용하여 힙의 루트 값을 꺼내어 배열의 오른쪽부터 채워넣으면서(오름차순 기준) 배열을 정렬할 수 있다. 힙으로 만들기 -> 배열의 맨 오른쪽부터 루트값 채워넣기 -> 다시 힙으로 만들기 -> 루트값 채워넣기 ... 이렇게 배열의 정렬이 완료될 때까지 힙 만들기와 루트값 넣기를 반복하여 정렬을 한다. 시간 복잡도 : O(NlogN) 힙으로 만들 때 걸리는 시간 복잡도는 O(NlogN), 힙에서 루트값을 꺼내는데 걸리는 시간 복잡도는 O(1) 이므로 힙 정렬의 시간 ..

LCS(Longest Common Subsequence) : 최장 공통 부분문자열 두 문자열에서 "공통되는 가장 긴 부분문자열"을 찾는 알고리즘 여기서 subsequence는 꼭 연속하지 않아도 되는 부분문자열이다. * 문자열에서 substring 과 subsequence의 차이 * 문자열 A가 있을 때, - substring : 문자열 A의 연속하는 부분 문자열 - subsequence : 문자열 A에서 연속하지 않은 부분 문자열(연속해도 되고, 연속하지 않아도 됨) 즉, 다시 한번 짚고 넘어가면 LCS 알고리즘은 두 개의 문자열에서 subsequence를 찾는 알고리즘이다. LCS 알고리즘은 DP(Dynamic Programming : 다이나믹 프로그래밍)을 이용한다. LCS 알고리즘은 예제를 보면서..

병합 정렬(Merge Sort) 배열을 두 개로 쪼개어서 정렬을 한 뒤, 다시 병합하는 작업을 반복하는 정렬 알고리즘 배열을 중앙을 기준으로 앞(left ~ center)과 뒤(center+1 ~ right)로 나눈다. 이 작업을 배열의 요소가 2개가 될 때까지 반복한다. 나누어진 두 개의 배열을 정렬한 뒤 하나의 배열로 병합한다. 이렇게 배열을 모두 정렬 및 병합하면 종료한다. 시간복잡도 : O(NlogN) 퀵 정렬은 최악의 경우 시작복잡도가 O(N²) 이지만, 병합 정렬은 O(NlogN)로 유지된다. [예제] 배열 arr의 요소가 5 9 3 1 8 6 4 7 2 일 때, 이 배열을 오름차순으로 정렬하기 먼저 배열 arr의 left = 0, right = arr.length -1 로 초기화해준다. le..

투 포인터 알고리즘 - 다른 방향 배열에서 두 원소의 합이 어떠한 값 X와 일치하는 경우의 수를 구할 때 사용하는 알고리즘 단, 다른 방향 진행 방법에서는 배열이 정렬된 상태에서 가능하다. 배열이 2개가 존재할 때, 배열 하나는 포인터가 왼쪽에서부터 시작하여 오른쪽으로 이동하고 다른 하나는 포인터가 오른쪽에서부터 시작하여 왼쪽으로 이동한다. 배열을 1개 사용할 때, start 포인터가 왼쪽에서 하나씩 증가하고 end 포인터가 오른쪽에서 하나씩 감소했던 것과 동일한 방식이다. 사실 배열이 한 개든, 두 개든 알고리즘 자체는 동일한데, 그냥 분리해서 이해하고자 따로 다뤘다. 투 포인터 알고리즘 - 다른 방향(배열 1개일 때) 투 포인터 알고리즘 - 2. 다른 방향(배열 1개) 투 포인터 알고리즘 - 다른 방..

퀵 정렬(Quick Sort) 알고리즘이 매우 빠르다라고 해서 붙여진 이름이다. 기준이 되는 피벗(pivot)을 설정하고, 그룹을 반복적으로 나누어서 정렬을 하는 알고리즘이다. 퀵 정렬은 피벗을 배열의 왼쪽 끝으로 설정하냐, 오른쪽 끝으로 설정하냐, 가운데로 설정하냐에 따라서 속도가 달라진다. 퀵 정렬의 알고리즘을 간단히 설명하면 이렇다. 배열의 왼쪽 끝 요소를 가리키는 커서를 pl, 오른쪽 끝 요소를 가리키는 커서를 pr 로 한다. 그리고 피벗을 가운데 값인 8로 한다고 하자. 피벗을 기준으로 왼쪽에 있는 구역을 A 구역, 오른쪽에 있는 구역을 B 구역이라고 할 때, A 구역에서는 pl을 오른쪽으로 이동시키면서 8보다 큰 값들을 찾아서 B 구역으로 넘기고, B 구역에서는 pr을 왼쪽으로 이동시키면서 8..

단순 삽입 정렬(Straight Insertion Sort) 선택한 요소를 그보다 앞쪽의 나열된 요소들 중, 알맞은 위치에 '삽입하는' 알고리즘 선택한 요소의 앞부분은 정렬이 완료된 상태이다. 삽입된 위치 이후의 요소들은 한칸씩 뒤로 밀려나게 된다. 알고리즘 : 배열의 두번째 요소부터 시작하여 하나씩 요소를 선택한다. 선택된 요소(arr[n])를 tmp 변수에 임시저장한다. * 변수 tmp에 임시저장하는 이유 : 왼쪽의 요소들을 한칸씩 오른쪽으로 미는 과정에서 선택된 요소(arr[n])가 있던 n번째 자리가 다른 값으로 채워지게 된다. 그렇게 되면 뒤에가서 arr[n]의 원래있던 값이 필요할 때 가져올 수 없으므로 tmp에 저장해둔다. 선택된 요소(tmp)보다 앞쪽에 있는 요소들(arr[0] ~ arr[..

단순 선택 정렬(Straight Selection Sort) 가장 작은 요소를 골라서 배열의 왼쪽부터 차례대로(오름차순 기준) 알맞은 위치로 옮겨서 정렬하는 방법 알고리즘 : 첫 번째 요소부터 차례대로 비교 기준(arr[n])이 된다.비교 기준의 다음번째 위치부터 마지막까지, 각각의 요소와 비교 기준이 되는 요소를 비교한다.더 작은 요소가 위치한 인덱스를 min 변수에 저장하면서 계속 min 변수를 갱신해나간다.마지막 위치의 요소까지 비교를 마치고 나면, 최종적으로 min 인덱스에 위치해 있는 요소(arr[min])와 비교 기준이 되는 요소(arr[n])를 서로 교환한다. 시간 복잡도 : O(N²) 버블 정렬, 삽입 정렬과 마찬가지로 시간복잡도가 크기 때문에 효율적인 정렬 알고리즘은 아니다. [예제] 배..